【情報Ⅰ】2025共通テストの詳しい問題解説①

デジタル署名の問題です。知識と言えば知識ですが、言葉からも想像ができますよね。
「署名」というのは、デジタルでもアナログでもそれが本人のもので間違いがないことを証明するために使用されます。

解答は3になります。
細かな話始めると「公開鍵」や「秘密鍵」の話が出てきますが、ここでは割愛しますね。

128ビットのIPアドレスが利用されるようになった理由を問われています。

IPアドレスはインターネットに接続する端末を1つに特定するために割り振られる住所のようなものです。これまではIPv4という32ビットで構成されるものを使用していました。

32ビットということは、1ビットは1か0の2種類ですから、32ビットは2³²個のIPアドレスを持てるということを意味します。2³²＝4,294,967,296(約42億個）となります。

32ビットのものを128ビットにするということは、2³²(約42億）個を2¹²⁸個にまで増やすということを意味しています。

2¹²⁸＝340,282,366,920,939,000,000,000,000,000,000,000,000（約340澗（かん））という途方もない（0を数えることもイヤになるくらいの）数のアドレスを持つこととなります。

これはスマホなど、インターネット上に接続される端末が爆発的に増え、当初の想定のIPアドレス数では賄いきれないことから新しく規格を作り直したというものになります。

正解は2となります。

Nuro光など高速通信のインターネット接続サービスはIPv6を使用しています。

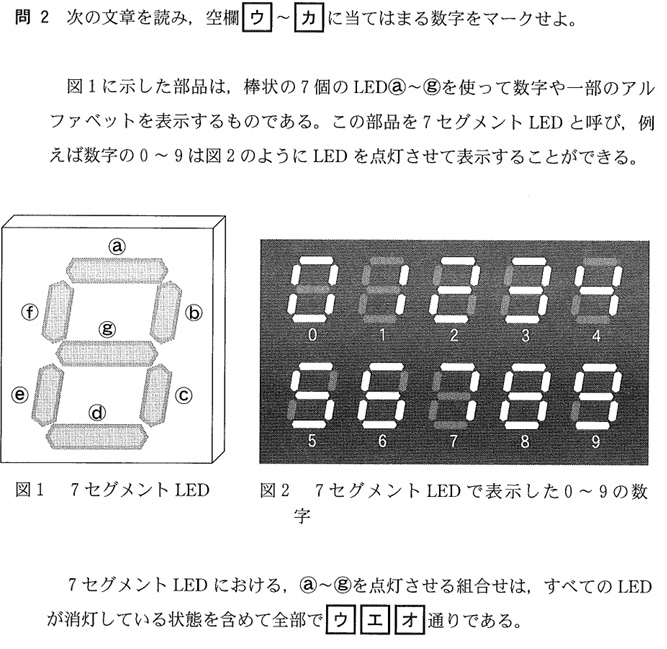
問２はウ～オとカを分けて解説します。

数字やアルファベットを表すために使われる7セグメントLEDの例を取り上げています。壁掛けのデジタル時計などで使われていることが多いですね。
情報の観点の一つに日常生活と紐づけて考えるというのがありますが、その一環ととらえればよいでしょう。

ここで問われているのは、上記の7セグメントのLEDを点灯させる組み合わせ数です。情報というよりは中学数学の問題です。

7セグメントにはaからgまでの7つのLEDがあり、それぞれが点灯または消灯の2種類情報表示が可能です。

a:点灯 or 消灯
b:点灯 or 消灯
c:点灯 or 消灯
d:点灯 or 消灯
e:点灯 or 消灯
f:点灯 or 消灯
g:点灯 or 消灯

つまり2つのパターンを持つLEDが7つということになりますから、2⁷となりますね。

2⁷は128ですので解答は、
ウ：1
エ：2
オ：8
となります。マークミスをしないように注意しましょう。

情報の問題は解答の割に読む量が多くて面倒ですね。

さて、問２のカですが、問題の条件を整理すると以下のことを問われていることがわかります。

◆7セグメントLEDは数字以外に以下の情報を表示できる。
・アルファベットの大文字8種類
・アルファベットの小文字5種類

◆以下のようにエラーコードを表示したい。
・1桁目に大文字アルファベット
・2桁目に小文字アルファベット
・3桁目以降は数字
・エラーコードは5000種類

◆5000種類のコードを表示するにはLEDが何個あればよいか

1桁目で8種、2桁目で5種表示できますから、最初の２つのLEDで
5×8＝40種類表示できます。

3桁目以降は10種類の表示ができる数字となります。
仮に数字部分が2個だと10×10（10²）で100種類表示が可能です。
アルファベット部分が40種類でしたから、40×100で4000種類表示可能となりますね。ところが、求められているのは5000種類ですから4000では不足します。
つまり数字部分は3個必要とわかりますね。

計算式にまとめると、以下のようになります。
8×5×10^X≧4000
X ＝ 3

よって、正解は3となります。

これも問題文が長くて少し大変ですね。
まずはキから考えましょう。

チェックディジットは複雑な計算をしてもミスが発見できないケースもあり、いろいろなパターンが研究されています。この問題でも、その工夫について問われていますね。

問題の趣旨は以下の通りです。

クの入力ミスの場合、
生成方法Aではミスの検出ができないが、
生成方法Bではミスの検出ができる。

つまり、AとBの違いで何のミスが検出できるかということが問われています。

生成方法AとBの違いを比較すると、相違点は以下の1か所のみです。

生成方法Aはすべての桁の値を足す
生成方法Bは奇数桁の数値を3倍してから足す

奇数桁のみ3倍すると何ができるかという観点で選択肢を見てみましょう。
奇数桁と偶数桁を入れ替えて入力してしまった場合は明確にチェックディジットの値が変わります。

しかし、偶数桁と奇数桁を2つ間違えてしまった場合は、計算結果がたまたま同じ数値になってしまう可能性もありますよね。
たとえば、22609を22469などと、2カ所間違ってしまった場合はチェックディジットがともに7となってしまい検出ができません。

よって、正解は3となります。

問４もケから考えてみます。

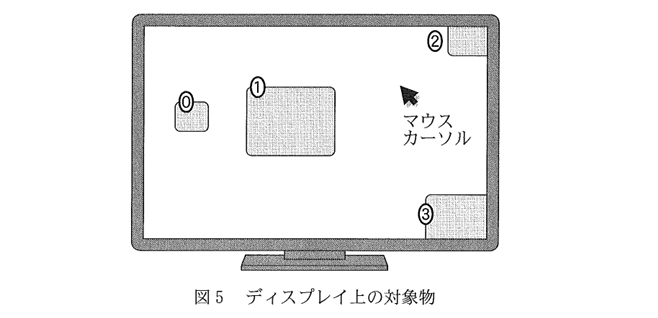
情報デザインの考え方に関する問題です。ユーザーインターフェース（UI）を考える際の法則を例にとって、考え方を整理していますが、問題文をきちんと読めれば容易に解答できるのではないでしょうか？

問題の趣旨を整理します。

【UIデザイン上の法則】
・対象物が大きいほど、対象物に移動するときの時間が短くなる
・対象物への距離が短いほど、対象物に移動するときの時間が短くなる

【追加情報】
・ディスプレイの端にある対象物は実質的に大きさが無限大になると考える

【問題の趣旨】
・図5のディスプレイ上の対象物で最も短い時間で差し示せるものを答える

【UIデザイン上の法則】に当てはめると、
・距離が一番短いのは2（1もかなり近いが）
さらに【追加情報】を意識すると
・最も大きい対象物は2と3
2はどちらの条件も満たし、最も短い時間で指し示すことができる

よって、解答は2となります。

ちなみに、この法則は「フィッツの法則」と言われています。「画面の端の対象物の大きさを無限大と考え、最も短い時間で指し示せる」という考え方に違和感を感じる人もいるかもしれません。
これは、端の対象物はマウスが通り過ぎることがないため乱暴にマウスを動かしても対象物を指し示せることを意味しています。実際に画面の上部や株にあるボタンは真ん中にあるボタンよりも押しやすいのではないでしょうか？