
こんにちは。共通テストの「情報Ⅰ」の解説をしています。
今回は第3弾、大問2のBを解説します!
- 共通テストで新科目「情報Ⅰ」がスタート。
- 現時点では、全体の配点に占める割合は低く、大勢に影響はなさそう。
- 今後少しずつ配点が高まるので、現高1や中3くらいからは留意が必要。
大問2Bの解説
大問2の概観
大問2は「情報通信ネットワークとデータの活用」と「コンピュータとプログラミング」から出題でした。慣れていないと少し難しく見えるかもしれませんが、各問題で与えられた数値の意味が見えればここもそれほど難解というものでもないと思います。
大問1同様、手際よく充てられた問題の趣旨を理解できるかの方が重要だと思います。
大問2 B 問題文


Mさんが10人のメンバーから現金で6000円を集める際のお釣りをシミュレーションするという問題です。
今は現金じゃなくて、Paypayでしょう!という突っ込みは呑み込んで…(笑)
条件を見ると、1000円札6枚か10000円しか払わないという受験生向けの条件になっていますね。その他の条件も問題文をよく見て整理しておきましょう。
では、各問題に入ります!
問1
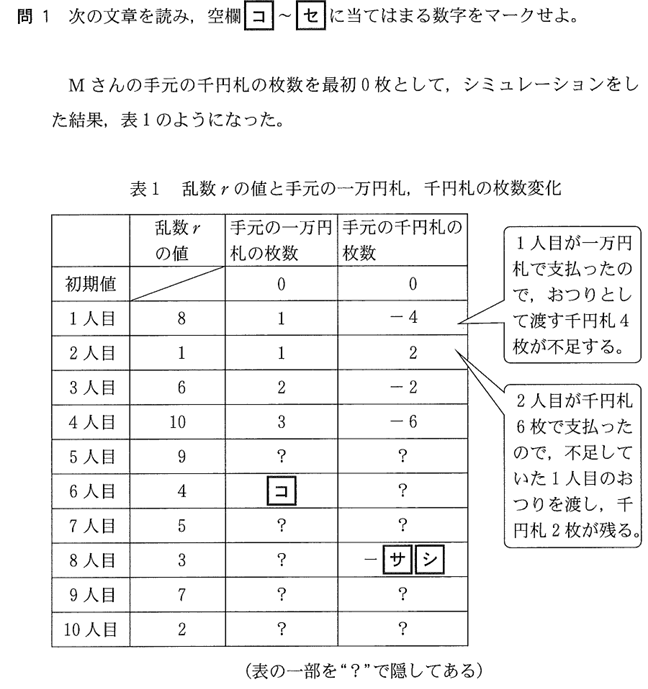


コ~セに入る数字を答えるという問題です。
rは問題文の条件で記載がされていましたね。
rが3以下:千円札6枚で支払う
rが4以上:一万円札1枚でで支払う
となっていました。
条件を整理すれば比較的簡単に答えが出ると思います。
表のrの値と一万円札の枚数と千円札の枚数の関係を整理すると以下のようになりますね。
| 乱数rの値 | 手元の一万円札の枚数 | 手元の千円札の枚数 |
| 3以下の場合 | 変化なし | +6枚 |
| 4以上の場合 | +1枚 | -4枚 |
上記の通り、お札の枚数が変化しますから表の開いているところに数字を埋めて解答を出せばよいわけです。
難易度を上げるためにコの上に「?」などが入っていますが、それも含めて票を埋めてしまうとよいと思います。
コ
5人目も6人目もrの値が4以上ですから1万円札で支払いますよね。
4人目の段階で1万円札は3枚ですから、2枚増えて5枚になりますね。
コの正解は5となります。
サシ
4人目の段階で千円札は-6枚
5人目~7人目までrの値はいずれも4以上ですから、
7人目までで、-6+(-4)×3=-18枚となっているはずです。
8人目のrの値は3なので、千円札が6枚入ってきます。
-18+6=-12となっているはずです。
サシの正解は 1 2 (サ=1、シ=2)となります。
スセ
今回1回だけのシミュレーションで必要な千円札の枚数を答える問題です。
サシまでで-12枚となっていますが、その後のシミュレーションも終えておく必要がありますね。
9人目:rが7なので千円札は-4枚
10人目:rが2なので千円札は+6枚となります。
この表を一度すべて埋めてみて千円札の最小値を確認してみましょう。
| 乱数rの値 | 手元の 一万円札の枚数 | 手元の 千円札の枚数 | |
|---|---|---|---|
| 初期値 | ー | 0 | 0 |
| 1人目 | 8 | 1 | -4 |
| 2人目 | 1 | 1 | 2 |
| 3人目 | 6 | 2 | -2 |
| 4人目 | 10 | 3 | -6 |
| 5人目 | 9 | 4 | -10 |
| 6人目 | 4 | 5 | -14 |
| 7人目 | 5 | 6 | -18 |
| 8人目 | 3 | 6 | -12 |
| 9人目 | 7 | 7 | -16 |
| 10人目 | 2 | 7 | -12 |
となりますね。千円札の不足が一番大きいのは7人目の-18です。
よって、スセの正解は18(ス=1、セ=8)となります。
問2
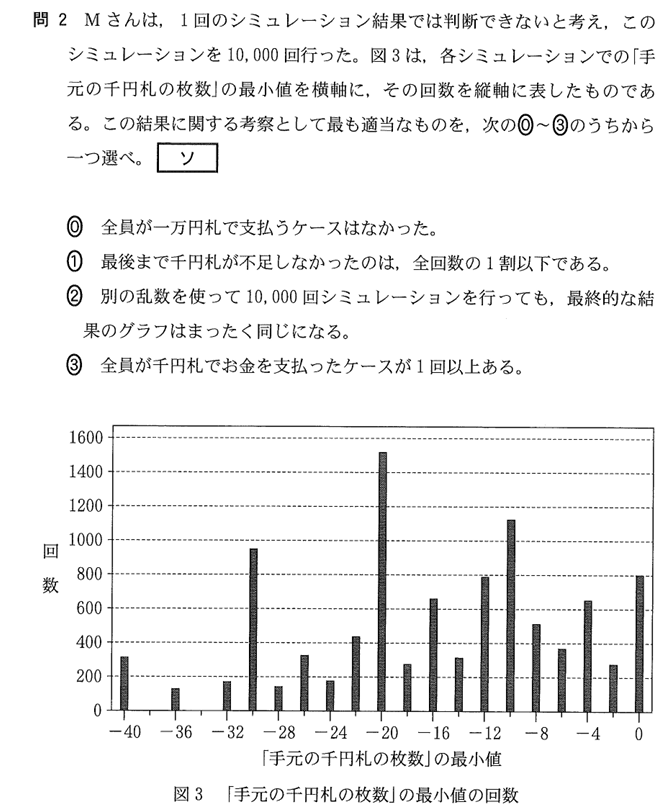

Mさんがシミュレーションを10,000回行った場合の結果を表したグラフを読み取る問題です。
グラフの読み取りではグラフの各項目が何を表しているかを確認することが重要です。
縦軸:回数
横軸:「手元の千円札の枚数」の最小値
となっていますよね。
例えば、一番右の横軸が「0」の棒グラフは、
10,000回中およそ800回は「手元の千円札の枚数」最小値が0だったということです。手もとの千円札の最小値が0ということは、千円札が1枚もなくても集金が完了したということを表していますね。
逆に一番左の横軸が「-40」の棒グラフは、10,000回中およそ300回は千円札が-40手元にあった(=40枚不足していた)ということを表しています。
このような考え方をもとに選択肢を見てみましょう。
0:全員が一万円札で払った場合は、-4枚×10人で-40枚千円が必要です。グラフ上に-40がありますので、全員が一万円札で支払ったケースはあります。
1:最後まで1000円札が不足しなかったということは、千円札が0枚でよかったというケースです。この回数は約800回で10,000回の約8%に当たり、選択肢に記載されているの10%以下に合致します。正解です。
2:別の乱数を使ってシミュレーションをしたら、元となる数値が異なるので結果グラフも異なりますよね。これは不適切です。
3:全員が千円札で支払ったケースはこのグラフ上では「0」のところに当たるので選びたくなるかもしれませんが、「0」が表しているのは「手元の千円札の枚数」の最小値です。例えば千円で払った人が最初に1名いてその後に一万円札で払った人が出てきても最初にもらった6枚の千円札で支払いができるため、「0」は全員が千円札で支払ったことは表していません。これは不適切です。
正解は1となります。
問3


Mさんが20枚千円札を要した場合に起こることがないケースを選ぶ問題です。
これも選択肢を一つずつ見ていきましょう。
選択肢で与えられた状況が起こる極端なケースを想定して消し込むとよいでしょう。
0:最初の1人が千円札で払うと千円札は6枚ですね。もともとあった20枚と合わせて26枚となります。残りの9名がすべて一万円で払った場合、千円札は4枚×9人で36枚必要となるため、このケースは起こり得ます。
1:用意した千円札を全く使うことなく集金を終えるケースは、全員が千円札で払えば起こり得ます。
2:千円札で支払った人が5人いて、お釣りが不足するケースは、最初の5人が全員一万円札で払った場合を考えるとよいでしょう。5人が一万円で払うとお釣りは千円札4枚×5人で20枚必要です。もともと用意していた千円札20枚はすべてなくなってしまいます。しかし、その後の5人は全て千円札で支払うので、千円札は不足しませんね。よって、ここの千円札が不足するケースは起こることがありません。正解です。
3:一万円札で支払った人が8人いて、お釣りが不足しないケースは、最初に8人が千円札で払った場合を考えます。その場合、千円札は「元の20枚」+「2名が支払った12枚」で、合計32枚となります。その後8人が一万円札で支払うと、千円札は4枚×8人=32枚必要で、手元の千円札でちょうど集金を終えることができます。よってこのケースも起こり得ます。
上記の通り、正解は2です。
まとめ
大問2のAよりはむしろ取り組みやすかったのではないかと思います。
それぞれの数値が何を表しているのかを把握し、わかった数字をどんどん埋めていくようにすれば全体の様子が見えて解答のスピードも上がるでしょう。
情報は、問題形式に慣れることが大事です。対策問題集などで類似の問題を経験することをお薦めします。
大問3の解説記事もできましたら追加投稿します。
以下に共通テストの情報の問題集をご紹介しておきます。




コメント