
こんばんは。まさおです。
各都道府県の公立高校入試の出題範囲が続々と発表されています。例年と同じ範囲で行う自治体もある一方で、首都圏や大阪を中心に出題範囲を縮小するところも出てきています。
特に数学では「三平方の定理」を出題しないところが多いようです。
今回は「三平方の定理のない入試数学」というのを考えてみます。
三平方の定理は高校入試数学でも正答率の低い問題で出やすい
⇒三平方の定理が出ないということは難問に出会いにくくなる
来年度の数学の入試問題は以下のどちらかになる可能性が高い
⇒①三平方以外の図形問題などに難問を持ってくる
⇒②数学は差がつきづらくなり他の教科が合否に影響を与える
令和2年度都立の数学の問題をチェック
まずは令和2年度の公立入試の内、代表的な都立の共通問題を見てみましょう。
問題は以下のページからダウンロード可能です。
https://www.kyoiku.metro.tokyo.lg.jp/press/press_release/2020/files/release20200221_01/2s_kensa.pdf
ちなみに、東京都が発表した平均点は61.1点でした。
東京都は毎年6月にその年の2月の入試問題の分析資料を公表しています。今年も以下のような資料を公表しています。
https://www.kyoiku.metro.tokyo.lg.jp/press/press_release/2020/files/release20200625_01/houkoku.pdf
これをベースに、令和2年度の入試問題から三平方の定理が絡む問題がどういう問題化を確認してみましょう。
良い入試問題の条件
受験生の中には入試問題の見方がまだわかっていない人がいるかもしれませんので、最初に少し解説をしておきます。
「良い入試問題」というのは、受験生の学力差が点数によくあらわれる入試問題のことを言います。
そんなの残酷だと思うかもしれませんが、入試というのは合格者と不合格者を分けなければなりません。
そのため、どの教科もよく理解している人が高得点となり、よくわかっていない人が低得点となるように入試問題を作ります。
そんなの当たり前ではないかという人がいるかもしれませんが、これが意外と難しいのです。なぜ難しいかというと、よく差のつく問題というのは正答率の高い問題から生徒率の低い問題まで、難易度を適切にばらつかせないといけないからです。

例えば、やさしい問題ばかりだったらみんなが高得点を取ってしまって差がつきませんよね。
逆に難しい問題ばかりだったら、多くの生徒が低い得点になってしまってやはり差がつきません。それでは合格者と不合格者を分けることができないのです…。
高い正答率の問題から引く正答率の問題までを適切にばらつかせながら、受験生の実力を得点に表すという職人のような技が入試問題を作る人には求められるのです。

ちなみに受験生の皆さんは、自分の実力に会った正答率の高い問題を確実にとることが合格への近道ということになります。
各小問ごとの正答率と三平方の定理が絡む問題
さて、それでは令和2年度の都立高校の数学の問題、どのような正答率だったか確認してみましょう。
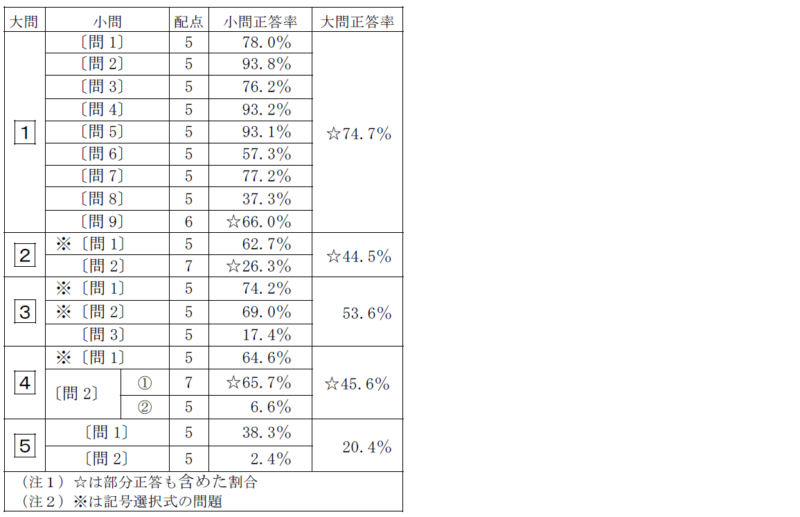
大問別の正答率を見てみると、大問1が74.7%、大問5が20.4%とうまくばらけていますよね。
小問正答率を見ても、
90%台…3問
80%台…0問
70%台…4問
60%台…5問
50%台…1問
40%台…0問
30%台…2問
20%台…1問
10%台…1問
10%未満…2問
となっています。90%台はすべて大問1の計算問題ですね。
三平方が絡む問題に色を付けてみると…
今回出題範囲から外れた三平方の定理が絡んだ問題に色を付けると以下のようになります。
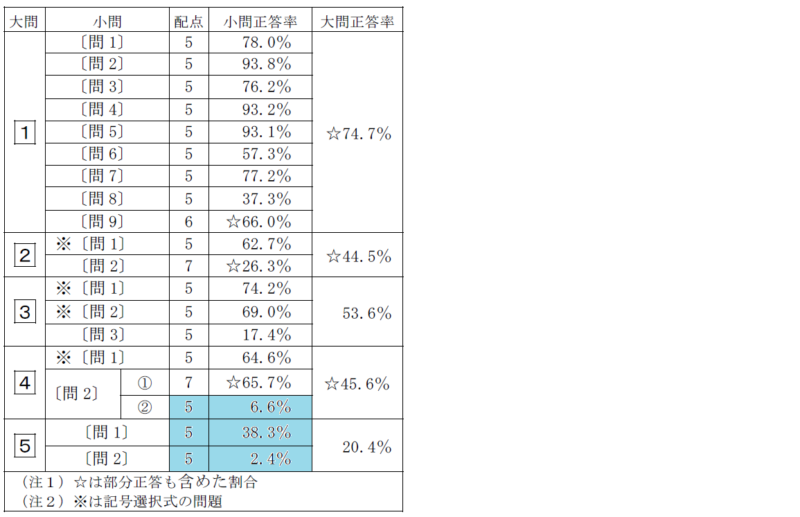
国語ばかりを教えていたので、久々に数学の入試問題を解いてみましたが、結局三平方の定理が絡んだのは最後の3問だけでした。
ところが、この3問、正答率を見てください!
10%未満となった2問はいずれも三平方の定理が絡んでいます。
つまり、「三平方の定理」は入試の最後の砦、最も差のつく問題で出題される最終兵器なのです。
これが出題されないとなると来年の入試はどうなるのでしょうか?
結局、来年度入試はどうなる?
ここから考えられる来年度入試の展開は大きく2通りです。
三平方の定理以外の問題の難易度を上げてくる
三平方の定理を封じられたとなると、出題者は他の問題で少し難易度を上げて正答率を下げる問題を作ってくる可能性が高いです。
他の問題の難易度をそのまま維持してしまうと、数学の差がつきにくくなるからです。
ただし、難易度を簡単に上がられるかというと簡単にはいかない可能性があります。下手に難易度を上げ過ぎると、今度は逆の意味で差のつかない(誰も解けない)問題になってしまうからです。
具体的には、2次関数か円の問題の難易度を上げることになると思います。ただし、関数の問題の難易度を上げると座標軸上に三角形ができて三平方の定理を使いたくなってしまいます。
意外と2次方程式の文章題などが出てくるかもしれませんね。

受験生の皆さんは学校や塾にの先生をフル活用して、三平方の定理が出ない入試問題の練習をぜひしてみてください。
数学で差がつきにくくなり理社がポイントになるかも
三平方の定理がなくなって、数学の難易度が下がってしまうと、結果的に理科や社会などの得点がものをいうようになるかもしれません。
入試は5教科の合計得点と内申点で決まるものです。数学の得点で差がつかない場合は他の教科で差がつくかもしれません。
その時に差がつきやすい教科は理科と社会です。
都立は英語も比較的ばらつきがあるようですが、一般的には理社のばらつきが大きくなる傾向があります。
令和2年度の理科の得点分布は以下の図の通りです。
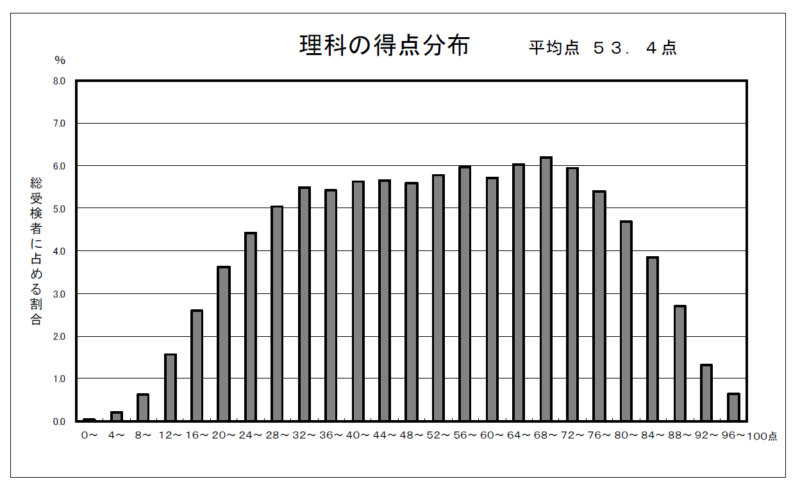
横に広い台形のような分布になっていますね。それだけ得点差が広がっているということが言えます。理社はもともと試験範囲内で覚えることが多い教科です。計画的に学習をして、確実に得点する力をつければそれだけ有利になりますので、ぜひ理社で得点できるように頑張って行きましょう!


コメント