
こんにちは。まさおです。
入試を考えるときに「偏差値」という言葉がよく出てきます。平均点の位置が50で、上限が70~75くらい、加減が25~30くらいというイメージだけ理解している人も多いと思います。
そもそも偏差値って何なのでしょうか?
その意味を知ると有効な使い方もデメリットもわかってきますね。
今回のテーマは「偏差値って何?」というテーマでわかりやすく解説します。
◆偏差値は母集団の中の自分の位置を表す指標
⇒一般的には模擬試験などで全受験者における自分の得点位置を示す
⇒平均点の50を中心に数字が高ければ母集団の中の上位に位置する
◆「母集団」と「試験問題」が非常に重要
⇒母集団のレベル自体が模試ごとに異なるので偏差値に互換性はない
⇒試験問題が難しすぎたり簡単すぎると正しい位置が測れない
※模試の位置づけを正しく理解しないと偏差値を読み誤る危険性も!!
偏差値をざっくりいうと!?
偏差値とは、統計的な手法をつかって、母集団の中の自分の位置を表した数字のことです。
よく見かけるグラフに表すと以下の通りです。
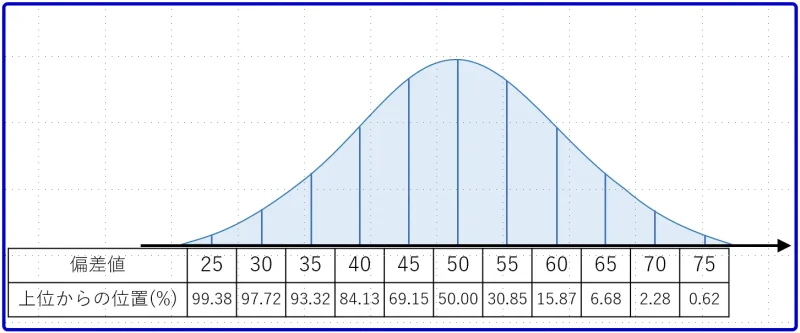
ポイントは、上位からの位置というところです。
たとえば、偏差値60と言われれば、母集団における上位15.87%あたりの位置にいるということになりますね。
上位15.87%というのは、学校のクラスが40名だとすると6位くらいの位置です。
偏差値60というのは、クラスの中でかなり優秀な位置にいるということですね。
40人クラスに当てはめて表にまとめると以下のようになります。
| 偏差値 | 40人クラスの 順位換算 | コメント |
|---|---|---|
| 75 | 0.248位 | 162名中1位の位置。40人学級が4クラス必要。 |
| 70 | 0.912位 | 1クラスに1名いるか、いないかの位置 |
| 65 | 2.672位 | クラスの最上位グループがこの位置 |
| 60 | 6.348位 | クラス内でリーダー的な5~6人 |
| 55 | 12.340位 | クラス内で頭がいい方と言われているグループ |
| 50 | 20.000位 | クラスの平均の位置 |
| 45 | 27.660位 | 平均より少し成績の悪い子たちが含まれる |
| 40 | 33.652位 | 勉強が苦手と言われる子たちの位置 |

上記の通り、偏差値が母集団の中の大体どの位置かを知っておくと、「偏差値60って少し頭がいいくらいだよね」なんて言うイメージは覆ってしまい、「偏差値60を超えるって相当スゴイじゃん」という話になってきます。
一方で、この議論で忘れてはいけないのは「母集団」です。母集団のそもそものレベルが異なると、偏差値の意味が全く変わってきてしまいます。
偏差値の計算方法
偏差値の計算方法は以下の通りです。
偏差値=(個人の得点-平均点)÷標準偏差×10+50
個人の得点から平均点を引いて、標準偏差で割った数字を10倍してから50を足すというものです。
なんとなく平均点との差を捜査しているというのはわかりますが、「標準偏差」とは何なのでしょうか?
標準偏差…得点のばらつき度合いを表す数値で、計算式は以下の通り。

高校数学を学んでいないと上記の数式の意味は分からないと思いますが、nは受験者数、xは1人ひとりの得点、xの上に-が引かれているところは平均点を表します。
標準偏差の数値が大きいほど、上位から下位までの得点のばらつきが大きいことを示し、数字が小さいほどばらつきが小さいという意味になります。

標準偏差については、計算式はともかく、個人の得点の散らばりを表しているということを理解しておきましょう。標準偏差の数値が小さいほど、平均点との差が小さくても高い(あるいは低い)偏差値が出てくるということになります。
母集団を意識することが大事
偏差値は数学の統計手法の一つですから、そこに感情のような要素は一切入っていません。
しかし、駿台模試は難しいとか、中学入試の偏差値と高校入試の偏差値は比較できないといったことがよく言われますよね。
模試による偏差値の格差というのは厳然と存在しています。その背景は母集団の違いです。
京都大学の模試別の合格ライン比較
母集団の違いが偏差値に与える影響を知る方法として大学の合格ラインを各模擬試験がいくつで出しているかという比較があります。
たとえば、京都大学について確認をすると以下のようになります。
| 学部 | 河合塾 | 駿台 | ベネッセ | 東進 |
|---|---|---|---|---|
| 総合人間学部 | 65.0~67.5 | 63.0~64.0 | 69.0~73.0 | 72.0 |
| 文学部 | 67.5 | 63.0 | 72.0 | 71.0 |
| 教育学部 | 65.0~67.5 | 61.0~64.0 | 69.0~70.0 | 71.0 |
| 法学部 | 67.5 | 65.0 | 73.0~76.0 | 72.0 |
| 経済学部 | 67.5 | 61.0~64.0 | 69.0~73.0 | 72.0 |
| 理学部 | 65.0 | 64.0 | 70.0 | 71.0 |
| 医学部 | 62.5~72.5 | 57.0~76.0 | 67.0~75.0 | 67.0~75.0 |
| 薬学部 | 65.0 | 64.0 | 70.0 | 70.0 |
| 工学部 | 62.5~65.0 | 60.0~64.0 | 67.0~70.0 | 69.0~71.0 |
| 農学部 | 62.5~65.0 | 60.0~63.0 | 67.0~69.0 | 68.0~70.0 |
学部の下に学科がある関係で偏差値に幅が出ていますが、之を見ると以下のようなことに気づきませんか?
- 駿台模試は合格ライン偏差値がかなり低く出ている
- ベネッセや東進は他の模試に比べて合格ラインがかなり高い
- 理系の学部よりも文系学部の方が偏差値が高い
これは母集団に違いが偏差値の違いに現れていると考えられます。
以下のような背景です。
模試を受ける受験生のレベル差
一般的に模試を受ける受験生のレベル差は以下のようになっています。
これは意図してそうなっているわけではなく、受験生が受験料を払って模試を受ける際にどの模試を受けたいかで自然と母集団が分かれてしまうということです。
駿台>河合塾>ベネッセ・東進
駿台模試は問題が難しいことで有名で、生半可な気持ちで受験すると、5点や10点といったのちの人生にトラウマとなるようなひどい点数を取ってしまうことがあり、受験生の間でも上位生以外は受験をしないことが多いです。
河合塾は中間的な位置で、一般的な国立上位から私大の中堅下位まで堅実な判定をしてくれるので定評があります。
ベネッセは学校で全員受験などをさせるケースもあり、母集団が多いことは良いのですが、レベルはどうしても駿台や河合よりは下がってしまいます。
東進も衛星予備校などを全国にフランチャイズ展開している関係で母集団のレベルが、駿台・河合に比べて下がる傾向にあります。

模擬試験によるボーダーラインの違いは、大学入試に限らず中学入試や高校入試でも顕著に出ます。
偏差値を見るときは必ず母集団のレベルにも目を向けるということが大事なのです。
問題の作り方も偏差値に大きな影響を与える
塾の先生の中には自前のテストを作って偏差値を算出しようという人がいます。
多くの場合は母集団が少ないことが原因でうまく偏差値が出せないのですが、もう一つ重要な要素として「問題の作り方」という視点があります。
偏差値がきちんと出る模試は難易度調整がうまい
偏差値は冒頭に出したグラフの通り、得点がきちんと分布することが前提で価値のある値が算定されます。
そのためには、難しい問題から易しい問題まで難易度に一定レベルのばらつきを持たせた問題セットを作ることが重要です。

正答率のばらつきは、そのまま得点のばらつきにつながり、ひいては受験者が正規分布するかということに直結します。易しい問題ばかりや難しい問題ばかりですと、得点のばらつきが出てこないので偏差値が正しく出せません。
たとえば、駿台模試などは問題が難しいために、平均点が30点くらいになってしまうことが間々あります。そうすると、その模試で70点くらいとってしまうと突出して高い偏差値が出てしまうのです。
もちろん、難関大学への合格可能性を図るという目的であれば難易度の高い問題で差がつくことが重要なのでこれでよいのですが、一般的なレベルの大学を受験しようとする生徒には不適切な物差しということもできます。
模試の特徴を知ってから偏差値を見ること
このように見てくると、「偏差値」と一言で言ってもその数字が持つ意味合いは大きく変わってくることがわかります。
ポイントをまとめると以下のようになります。
- 偏差値は母集団の中でどの位置にいるかを示す指標である
- 模擬試験によって母集団のレベルが異なるので偏差値に互換性はない
- 自分が受ける模試の母集団がどのようなレベルを知ることが重要
- 自分のレベルにあった適切な母集団の模試を受ければ偏差値は大変役立つ

偏差値の取り扱いについて、基本的な知識をきちんと身に着けておくようにしましょう。
正しく理解しておけば、正しく数字を扱うことが可能になります。


コメント